随着环境污染日益严重以及能源危机的加剧，清洁的可再生能源在电力系统中占的比重也越来越大，太阳能凭借其独有的优势成为新能源首选。因此，了解光伏发电系统的发电原理以及提高发电效率的方法是非常重要的。这里介绍了一个针对并网型光伏发电系统的MPPT算法。该系统采用单级式结构，省去了储能环节，拓扑结构简单，且效率高。

　　众所周知，光伏电池板作为光伏系统里很重要的组成部分，是整个系统能量的来源，不可或缺。但光伏电池容易受到外界温度、日照强度等环境因素的印象，使得其输出功率始终在发生变化。为了充分利用太阳能电池板并使系统能尽可能地稳定工作，光伏并网系统中最大功率跟踪技术的加入便显得十分必要。从电子系统方面考虑，对光伏组件进行最大功率点跟踪是降低发电成本、提高发电效率的最直接、最有效的方法。

　　1、光伏电池输出特性分析

　　光伏电池受外界因素（如环境温度、日照强度等）影响，输出具有强烈的非线性，其数学模型可表示为：

　　式（1）也即光伏电池的I-U特性关系，其中：I、U分别为光伏电池输出电流和端电压；A、B与PN结材料特性相关的系数；k为波兹曼常数；T为绝对温度；q=1.602*10-19C为电荷电量；Rs、Rsh为别为等效串联电阻和等效并联电阻。

　　将式（1）转化为工程化数学模型，并加入适当补偿银子，可建立光伏电池的软件仿真模型，对于该模型本文采用PSIM仿真软件来建立，并结合MATLAB软件对该模型的可用性和正确性进行验证，仿真结果如图1所示。

图1 太阳能电池仿真模块光伏特性曲线

　　由图1中的四张图我们可以得出如下两条关于光伏特性的结论：

　　（1）在光伏电池结温不变的情况下，光伏电池的输出最大功率随日照强度的增强而增大，且最大功率点对应的电压几乎相同；在日照不变的情况下，太阳能电池的输出最大功率随组件结温的升高的变化趋势与恒温日照变大情况下功率变化趋势相反，结温越大，太阳能电池能输出的最大功率反而越小，且最大功率点对应的电压也随着结温的升高而下降。

　　（2）在光伏电池结温不变的情况下，日照强度越大，光伏电池的短路电流也越大，恒流区对应的端电压区间也越小；在日照不变的情况下，光伏电池的结温几乎不对短路电流产生影响，随着温度的上升极板的输出短路电流只是略有增加，而光伏电池的开路电压则随着电池结温的升高而下降，且下降幅度较大。

• 　　2、单级式光伏并网发电系统

  　　2.1、单级式光伏并网发电系统拓扑

  　　单级式的光伏并网发电系统由光伏阵列、DC-AC环节及滤波环节等构成。控制部分则主要有最大功率点跟踪控制及你变控制，前者控制系统工作于光伏阵列的最大功率点，后者控制直流到交流的逆变过程。其拓扑结构框图如图2所示。

  

  图2 单级式光伏并网系统结构框图

  　　2.2、最大功率点跟踪控制策略

  　　早期的最大功率跟踪采用固定电压法（CVT）实现，虽然能保证系统稳定工作，但却无法使系统真正工作于最大功率点，造成了大量的能量损耗。近年来，随着数字控制技术的发展，MPPT逐渐引入到光伏并网系统中，目前，国内外研究的MPPT控制算法很多，如扰动观察法（P&O）、电导增量法（INC）、滞环比较法等，另外，为了提高系统的鲁棒性，许多学者把一些智能控制算法引入到MPPT中，如人工神经网络法、模糊控制法等，这些算法都有着各自的一些优缺点和适用场合。

  　　普通的MPPT控制算法多为一阶的控制策略，通过改变相关的控制量，使得光伏阵列的输出功率或一些相关变量发生变化，通过判断变化前后这些变量在曲线上的位置确定下一步的控制方式，从而使得系统工作点逐步向最大功率点靠近。这种控制方式在双级或离线式的光伏逆变器中是可行的，但是在单级式的光伏并网系统中一阶的MPPT控制策略稳定性差，将会导致母线电压崩溃或输出功率振荡，系统无法正常工作。

  　　早期的CVT法虽然无法真正寻优到最大功率点，但其稳定性高，而常规的MPPT控制算法虽能寻优到最大功率点，但稳定性差，因此，为了兼顾系统稳定性和功率点寻优的准确性，本文将CVT法与一类改进扰动观察法结合，提出了一种新的适合单级式光伏系统的MPPT控制策略，考虑光伏阵列工作点易随环境幻化而变化，因此本文的CVT采用模糊PI来实现，为了便于下文说明，这里将此法简称为FPO-MPPT，其控制框图如图3所示。

  

  图3 FPO-MPPT控制框图

  　　FPO-MPPT算法的核心思想是稳压为主，控流为辅。即系统正常工作过程中首先要确保母线电压的稳定，在母线电压稳定的前提下再去调节输出电流以控制回馈到电网的功率。这样便可保证在光照变化相当剧烈的情况下，系统也能稳定地向电网回馈电能，不致因母线电压的崩溃而使系统停止供电。

  • 　　3、模糊PI控制器设计

    　　3.1、模糊化

    　　模糊控制中的被观测量通常是一个在一定精度范围内的精确数值量，而模糊控制的操作是基于模糊集合理论的，因此，要进行模糊操作首先要对被观测量进行模糊化，模糊化必须按照一定的隶属度函数来进行，定义输入量的隶属度函数通常由三角形、梯形和吊钟型，理论上来讲吊钟型最为理想，但在工程上实现时计算复杂，可操作性不强。实践证明，用三角形或梯形函数的实现性能与吊钟型的并没有十分明显的差别，真正对控制器性能影响较大的是隶属度函数对论域的覆盖面大小，考虑到隶属度函数曲线的简单化和芯片处理的方便化，工程商常用三角形或梯形的隶属度函数来对输入量进行模糊化。

    　　对于本文的系统，要求输入偏差绝对值lel小余20%，取量化的基本论域为[-6,6]，总共13个量化等级，量化因子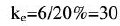，并对量化结果进行四舍五入运算，取偏差e在论域上的语言集合为{NL,NM,NS,Z,PS,PM,PL}。

    　　对于偏差变化率的绝对值|lel|，要求其不能大于6，取量化的基本论域为[-6,6]，总共7个量化等级，量化因子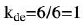,同样，要对量化结果进行四舍五入运算，取偏差变化率|e|在论域上的语言集合为{NL,NM,NS,Z,PS,PM,PL}。

    　　对输入输出的隶属度函数曲线都选为梯形，如图4所示。

    

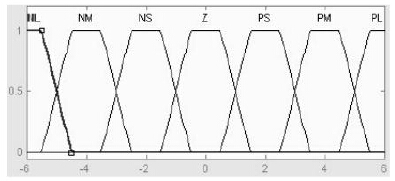
    图4 隶属度函数曲线

    • 　　3.2、确定模糊规则

      　　模糊规则用来修正PID控制器的参数，因此，模糊规则表的选取十分重要。模糊规则推理的输入输出都是模糊量，不同的模糊推理的出来的结果是不一样的，而采用不同的模糊推理方法，语言变量的分档也是不一样的。模糊推理方法有Zadeh法、Mamdani法和Baldwin法等，本文采用Mamdani发，也即MAX-MIN法来进行模糊推理，其方法为：分别在不同规则中采用各自推理的前件的总隶属度去切割本推理规则中后件的隶属度函数以得到输出结果，最后对所有的结论进行模糊逻辑并运算，得到总的推理结果，简单来说就是：前件取极小值，后件取极大值。

      　　根据PID调节规律，结合实际光伏阵列的端电压与输出电流的关系情况，得到表1所示的调节规则表，其中表1（a）为|Kp|的模糊规则，表1（b）为|Ki|的模糊规则，这些规则都是用模糊语言量来表示的。

      表1 模糊PI控制规则表

      （a）|Kp|规则表

      

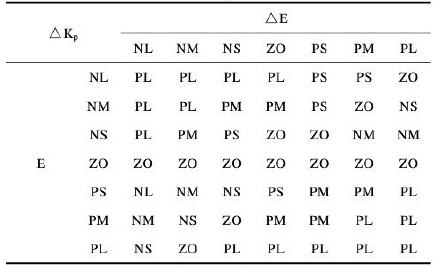
      （b）|Ki|规则表

      

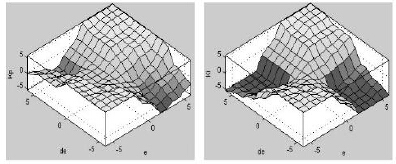
      　　运用MATLAB的模糊工具箱，画出本文的模糊控制器的非线性关系曲面图，其中图5（a）是|Kp|与e、|e|的关系，图5（b）是|Ki|与e、|e|的关系，普通PID调节器在xyz三维空间里是一张通过坐标原点的平面，其具有线性调节规律，而模糊控制器在三维空间中是一张通过原点的分片二次曲面，整张曲面毕竟一个阶数可以很高的非线性调节规律，故其整体控制效果要优于普通的PID调节器，模糊控制器在控制过程中的前期阶段具有模糊控制器的全部优点，而在控制过程的后期阶段又具有PID调节器的所有优势，因此是一种性能良好的控制器。

      

      　　3.3、反模糊化

      　　经过模糊推理后的结果是一些语言量的模糊结果，这种结果是无法对精确的模拟或数字系统进行控制的，我们必须进行反模糊化，通过精确化计算得出此模糊集中最有代表意义的确定值作为系统的控制输出。反模糊化有很多种不同的方法，如重心法、最大隶属度法、中位数法等，重心法不仅有公式可循，而且理论上比较合理，它涵盖利用了模糊理论的所有信息，并根据隶属度的不同而有所侧重，因此本文选用重心法作为反模糊化的方法。